この記事は、stanでモデルを組むことは出来てとりあえず走らせたけれどもRhatが1.0になってくれない。モデルの改良なり、サンプリングパラメータの調整で切り抜けたいが、「stanのマニュアルを読んでも、わかんねー」と思った時にどういう役に立てばと思います。
実際にはHMC(ハミルトンモンテカルロ)一般の話なので、pyMCとかでも事情は一緒ですが、Stanが使っている語彙で説明します。具体的には以下のパラメータや警告の意味が「わかんねーよ」っていうのに対して簡単な事例で説明したいと思います。
なお、この解説の元ネタとなっている論文はこちらです、ただ此方だと直接stanのパラメータ・警告とは直接結びついてないので本文書を書きました。https://arxiv.org/pdf/1701.02434.pdf
- sampligパラメータ
- stepsize
- stepsize_jitter
- metric : str, {“unit_e”, “diag_e”, “dense_e”}
- adapt_delta
- よく見る警告
- max_tree_depth
- E-BFMI
- divergence(adapt_delta/stepsizeに関連)
実験結果ソース
実験に使ったpythonソースは以下にて公開しています。自由に使って貰って構いません。HMC自体を実装しているのでstanは使っていません。
実験では2次元のパラメータqがガウス分布等に従う場合を例にサンプリングしています。多次元のサンプリングを1次元に射影した図で説明する文献が多いのですが、上のようなパラメータを理解するには、2次元ぐらいで具体的に見て行った方が解りやすいです。
https://akirayou.net/LeapFrogTest.html
前提知識
- MH(メトロポリスヘイスティング)法
- HMC(ハミルトニアンモンテカルロ)法
- stanのNUTS:HMCを効率良く運用する手法
NUTSだけ歯切れの悪い言い方していますが、stanでNUTSというと色んなパラメータ調整を行うwarmupを含めてNUTSと呼んじゃっているので、ググって出てくる所謂本家の「NUTS論文」とは違います。ただ、やってる事はHMCをうまく運用するためのパラメータの調整+サンプル数の動的な決定(後述)です。
なのでサンプリングがやりやすい(orやりにくい)モデルというのは、HMCアルゴリズムとの相性で決まります。
雑にMH法
MH法の詳細はググって貰うとして、有るパラメータθの確率密度pがあるとします。目標はp(θ)の分布に従う乱数を発生させる事です。このときの手法としてMCMC(マルコフチェーンモンテカルロ法)があるのですが、MHはその手法の一つです。
MCMCは適当なパラメータθからスタートして、「特定のルールでθを変更(遷移)」する事で、遷移の度に得られるθを記録するとp(θ)に従う乱数になっているという方法をとります。θが一次元だと総当たりできるので一様に発生させたθをp(θ)の確率で採用すればいいのですが、多次元になると総当たりが不可能なのでMH法を使います。
MH法では、その特定のルールとして「確率に基づいてθを遷移」します。具体的には遷移前の確率をp(θ)、遷移後のパラメータθ’の確率をp(θ’)として、「p(θ’)/p(θ)」の確率比に基づいて遷移するかしないかを決めます。なお1を超える時は単に「必ず遷移する」となります。この時遷移候補はθ’は全域に到達しうる分布からであれば、どんなに歪んだ分布からであっても適当に選んでOKです。「p(θ’)/p(θ)」のルールで叩き落とすので、候補の選び方は比較的どうでも良いのが特徴です。
雑にHMC
HMCはMH法の「適当に選んでOK」の部分に着目して、できるだけ効率よく選んであげようという手法です。具体的には「p(θ’)/p(θ)」に叩き落とされないように旨くθ’を選んであげようというものです。p(θ)=p(θ’)のとき必ず遷移できるので、これを制約条件にしてθ’を提案すれば良さそうです。だけどそれだと「全域に到達しうる」という条件が満たされません。
ここでθと同じ次元数の補助的なパラメータrを導入します。rはθとは独立だとします。この補助的なパラメータrを含めたp(θ,r)=p(θ)*p(r)について考えます。p(θ,r)の分布からサンプリングが出来たとすると、rについてθは独立なので単にサンプリングデータセット(θ,r)からrを無視するだけでp(θ)をサンプリング出来た事になります。p(r)については正規分布は、既知の高速な計算方法でサンプルを発生させる事ができます。そこで以下の遷移方法を行うのがHMCです。
- 適当なθ,rでスタート
- 更新候補r’を正規布乱数で発生させる(この時点で元のr消えてる)
- p(θ,r’)と同じになるp(θ’,r’)の中から(θ’,r’)を選ぶ
- p(θ’,r’)/p(θ/r’)=1なので、MH法的に遷移できる
今回はp(θ)を一定に保つのではなく、p(θ,r)を一定に保つ経路を考えて遷移しています。rはθと独立なのでθの遷移を決定する前に更新してしまっています(ギブスサンプリング)。その後p(θ,r)一定になる条件で遷移しています。p(θ,r)は乱数rでp(θ,r)の値を決定して、その後θをサンプリングするという二段階のサンプリングを行う事で、MH法の「確率的に基づいた遷移」と「全域に到達しうる」の両方を達成しています。ここでp(θ’,r’)=Const.となる(θ’,r’)を軌道と呼んだりします。これはθを「位置」として、log(p(θ))を位置エネルギー、rを速度(=運動量:モーメンタム)として、log(p(r))を運動エネルギーとして運動方程式をとくと、軌道を描きながら運動するけれども全体のエネルギーは維持される。性質を利用して一定のままr,θを動かすという計算をやっている事から「軌道」と呼びます。この全体エネルギーの事をハミルトニアンH(θ,r)と呼び、p(θ,r)=exp(H(θ,r))となります。 (厳密には計算の都合上=じゃなくて∝ )
イメージとしては確率分布がlog(p(θ))の形をしたお椀です。ガウス分布だったら二次関数的な形状をしたお椀です。そこにビー玉を入れて初速rで打ち出します。するとビー玉はお椀の中をグルグル回ります。適当な所で止めてその位置θを記録して、またランダムなrで打ち直します。処理は簡単ですね。何故それでp(θ)がサンプリングできるかは「MH法に立ち返って考えるとできる。」という事で深追いしません。
HMCでの軌道の例
以下の説明では今回参考にした文献(https://arxiv.org/pdf/1701.02434.pdf)にあわせてターゲットとなる確率分布のパラメータをq,モーメンタム項をpをします。
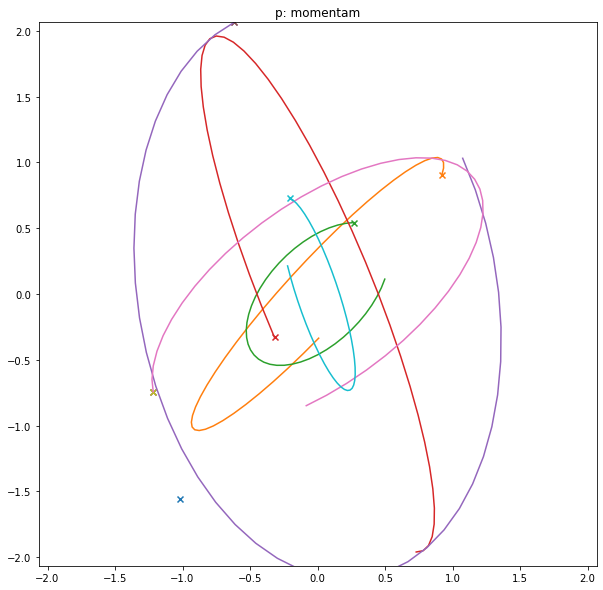
以下の図はターゲットの分布を正規分布とした時の例です。「×」マークがサンプル点です。パラメータqををよく見るとサンプル点(rが変更される点)で軌道が折れ曲がっているものの、一本に繋がっています。ビー玉を止めてサンプリングして、その場で方向・強さを変更して打ち直しているのでこうなります。

一方モーメンタム項pは速度なので、ビー玉を打った瞬間に値が変わります。ただ、qもpもガウス関数なので形自体はよく似ています。
効率のよいステップ幅で実行する:adapt_delta
上の例では綺麗な軌道を書くために運動(ハミルトニアン)方程式を解く際の時間のステップサイズを小さく設定していました。この運動方程式を解くのにはLeapFrog法という数値積分法(運動シミュレーション)を使っていて、急激に軌道が曲がる部分では誤差が乗ってしまいます。そのため実際のHMCではp(θ,r)=p(θ’,r’)を仮定するのではなく、ちゃんと計算して念のためその後差を含めた確率比をつかって遷移確率を設定しています。なのでステップサイズを大きくして誤差が大きくなると、遷移できる確率が減るというトレードオフになります。ソレを示しているのが元ネタの文献のFig33です。
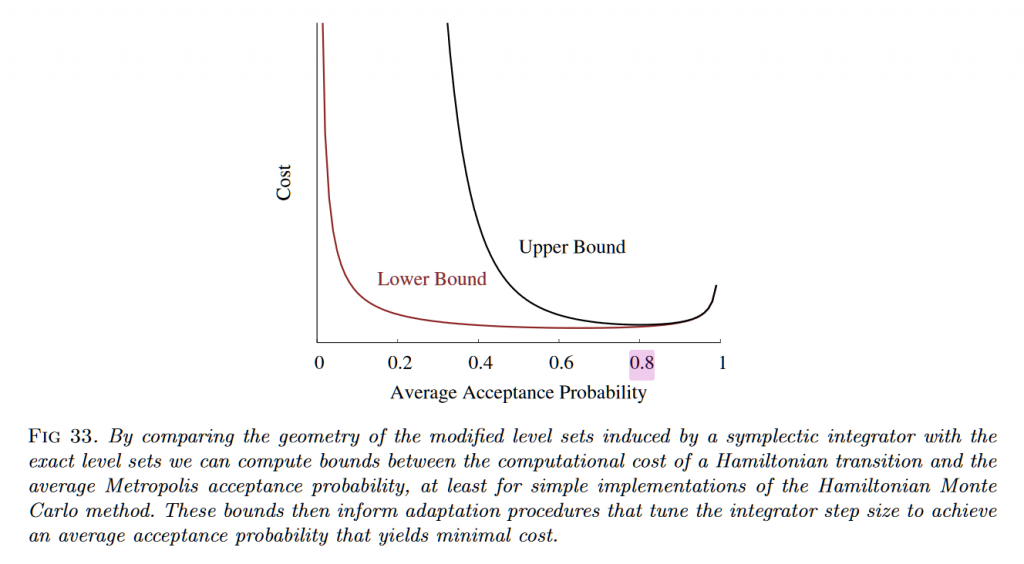
stanのNUTSでは最適な点としてデフォルト0.8の受け入れ確率(=adapt_delta)を目標にステップサイズを決めています。偶に警告でadapt_deltaを大きくすることで、step sizeを小さくしてねって言ってくるのはこの関係を知ってないと理解できないです。つまり受け入れ確率を上げるにはLeapFrogの誤差を小さくする必要があって、LeapFrogの誤差を小さくするにはステップサイズを小さくするのが手っ取り早いという事です。当然ながらstepサイズを小さくすると、同じ長さの軌道を計算するのに必要なステップ数(積分計算を行う回数)が反比例で多くなるので、計算量が増えてしまいます。
以下に受け入れ確率をおよそ0.8に手動調整したHMCの実行例を示します。わりとカクカクですが、軌道の形状はみえるね。って位です。ステップサイズが大きくなると、一回の移動量が大きいのでその分ステップ数が減らせます、以下の例だとLeapFrogのステップ数は4ステップです。

ステップ数について:max_tree_depth
stepサイズはwarmup段階で決定され、その後固定値として使われるのに対して、ステップ数はNUTSにより毎回必要な量を実行されます。このときの基準が「Uターンしない。」というものです。以下はステップ数を長く取ってみた実験例です。ガウスの場合はrによって決まる軌道は綺麗な楕円です。なのでステップ数を長くしても自分と同じ値に帰ってくる可能性が高いです。

ステップ数を大きくして、同じ値を拾うと無駄が多いです。かといって小さくしすぎると、一回のステップでは全域に到達できなくなって、効率が悪いばかりかMH法の「全域に到達できる」という指針も怪しくなります。
そこで、NUTSでは軌道を時間方向に正・負両方に確率的に伸ばしていて、Uターンしたらへんがちょうど良いだろうということで、Uターンしたら打ち切って、そこまでつくった軌道の中からランダムに次の候補を選ぶという事をやっています。「軌道の長さを打ち切る基準をもつ」、「最後の1点ではなく、軌道の中から選ぶ」という2つの工夫をやっていますが。後者はチューニングしようがないので前者だけが問題になります。この軌道は無限の長さを取るわけにはいかないのでmax_treeというパラメータで制御され、2のmaxt_tree乗のステップ数まで伸ばして調べるとしています。デフォルト値はmax_tree=10なので最大1024ステップまで見ます。max_treeに関する警告がでたときよく15等の数値に設定しますが、最大ステップ数を2^15=32768にするという事なので、計算時間には覚悟が必要になります。 ガウス分布だとステップ数4とかで良いのにmax_treeが巨大なのが必要になる理由については後述。
おまけ:stepsize_jitterとESS
上のセクションで「ステップサイズはwarmup次に決めて固定」と言いましたが、今回のような綺麗な分布の場合綺麗に円を描いてかつ、一週まわるのに必要なサンプル点数が8点程度です。運が悪いと軌道の中を綺麗に回りすぎて、同じ点ばかり集中的にサンプルしそうじゃないですか?こうなると100回サンプルしたのに実はそのうち半分は同じパタンがあって実質50回という事にも鳴りかねません。この実質のサンプル数をESS(有効サンプル数)と呼びサンプリングされた値の系列の自己相関ρlから計算されます。(ρlはl点離れたサンプルとの相関、つまり色んな周期で見て類似パタンが存在する度合いを足し込んでいる)
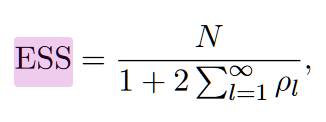
この綺麗な周期性のために起こる自己相関(=有効サンプル数)を防ぐのたsamplesize_jitterでステップサイズを0~1の範囲でランダム縮小して位相をあえてずらしてあげようとしています。周期性が綺麗でる分布では有効ですが、元より綺麗な周期性がでないようなぐちゃぐちゃとした位置エネルギー、すなわち複雑なターゲット分布をもつ場合は余り効かないはずです。
なお、ESSが極端に小さい場合はそのサンプル結果を信用してはいけません。stanのマニュアルではチェイン毎に100有る事を推奨しています。ただ対処方法として計算時間をかけてサンプル数を増やすという手が使えるのでESSをあまり深刻に気にしてる人はいないです。
歪んだ分布での挙動
ここまでは綺麗なガウス分布での話でしたが、歪んだ分布の例を見てみましょう。ガウス関数exp(-q**2)の代わりにexp(-|q|)やexp(-|q|^0.25)を使った裾の重い(遠くの裾まで確率がある)分布で、もう一つがガウス分布を伸縮・回転したものです。
裾の重い分布
裾の重い分布の例としてexp(-|q|)を見てましょう。同一の円じゃなくて少しずつズレなら円を描いていますね。こうやって軌道がずれていく事自体は特に問題ないです。NUTSでは開始点からすたーとして、初めてのUターンポイントで打ち切りますが、今回の実験ではそれよりちょっと長めにステップ数をとっています。パラメータq,モーメンタムpともに内側にある軌道すなわち確率が高い所の軌道がターン数が心持ち多くないですか?


非常に裾の重い分布
解りやすくするために、もっと極端に裾が重い軌道にしてみましょう。exp(-|q|**0.25)です。ターゲット分布のパラメータqは中心部では楕円状にに何回か回転できているのに、外側にある軌道は回転できていません。
一方でモーメンタム項pは所々軌道が非常に短い点が存在します。

物理に戻って考えると簡単です。-|x|**0.25のグラフは以下の形をしています。
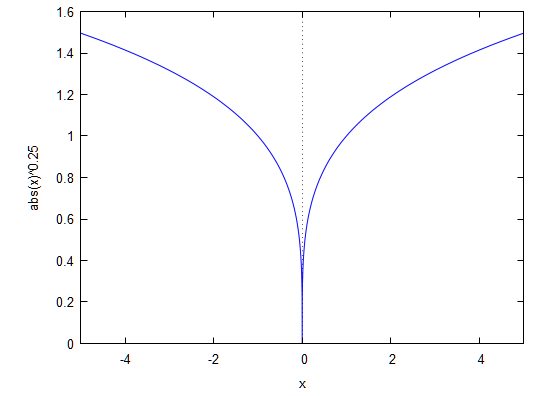
つまり漏斗の形をしたお椀にビー玉w転がすようなものです。漏斗の奥底でビー玉を転がせばあっという間にUターンして回転しますが、漏斗の外側では延々と真っ直ぐ進んで、中々Uターンしません。その状況では速度pの変化もあまりなくモーメンタム項pの軌道も短くなります。
結果としてターゲットパラメータqのスタート位置によって、必要なステップ数が大きく異なる事を示しています。
このため、warmupではお椀の底の都合もあり、比較的小さなステップサイズを設定しなければならないのに、たまにお椀の縁に行くと非常に長い軌道を要求されるためにステップ数が大きくなり、max_treeの制限を超えてしまう事になります。このように基本的にHMCは「裾が重い分布は苦手」なのです。
対策:再パラメータ化
この例に限ってしまえば対策は簡単です。ガウス関数なら綺麗にサンプリングする事ができるので、ガウス分布をサンプリングしてお椀の直径を8乗して後付けで漏斗形状にしてあげればよいのです。つまりガウス分布が得られた値xを8乗したq=x^8という変換をしてあげれば良いです。再パラメータ化というとNeal’sFunnelや階層化パラメータの例のように複数のパラメータが絡むものが有名ですが、stanのマニュアルでstudent T分布をガンマ分布に変換しているように今回のような裾の調整でも使えます。あくまでサンプリングされるp(stanでいえばparamter ブロックに書いてある変数群)がどんな分布になるかが大事なのです。(Neal’s Funnelや階層化についても知っておくべきですが、今回は略)
Divergenceってなんぞ?
Divergence(発散)に関するエラーが出たり、stanの結果を可視化するarvizでもDivergenceを可視化しながらパラメータqをプロットする機能があります。コレの意味ですが、LeapFrogで軌道を生成中に、全体エネルギーH(q,p)が変な値にぶっ飛んでしまった事を意味します。上の漏斗のような形の例の場合、q=(0,0) 付近に軌道が落ちるときの速度(モーメンタム項)ですごい大きな値になりそうですよね。
複雑なモデルになると、急加速ポイントが現れたりします。その際にLeapFrogの積分誤差がでるとH(q,p)が非常に大きな誤差をとって値がぶっ飛びます。そう言う場所qというのは位置エネルギーの曲率が極端に大きい事を示しています。
モデルを改良する場合にはそういった極端に曲率がデカイ部分を解消する事も検討する価値があるのでstanはわざわざdivergenceが出た場所を記録しています。
なお、divergentの基準はstanのソースにあるように1000動いたらdivergentと決め打ちされています。
伸縮回転した分布
2次元の正規分布に以下のマトリックスMを書けたものを考えます。コレは回転縮小を空間にかけたと考えてもよいですが、2次元のパラメータの一つ目と二つ目が相関を持っていると考えても良いです。
M=np.array([[1,0.99],[0.99,1]])
結果を早速みてみましょう。ターゲット分布のqはMで設定した通り強い相関もっているので斜めに細長く分布しています。このときの軌道はリサージュ曲線(wikipedia)ぽい形になります。ウネウネしながら長手方向に移動する軌道ですね。⁽⁽(ી₍₍⁽⁽(ી⁽⁽(ી₍₍⁽⁽(ી( ˆoˆ )ʃ)₎₎⁾⁾ʃ)₎₎ʃ)₎₎⁾⁾ʃ)₎₎

注目はモーメンタム項pです。サンプル点が少なくて見づらいですが、サンプル点自体は正規分布になります。軌道が激しくウネウネしています。特定の方向ベクトルでいえば(1,1)方向に激しく振動しているためその端点で曲率が大きくなっています。LeapFrogがこの曲率が急激な所にある程度耐えられるようにするためにステップサイズを小さくする必要がありますが、その小さなステップサイズは、ほぼ直線に進む区間では無駄に小さなステップサイズとなります。結果としてステップ数が増大し計算が遅くなります。

対策:metric
stanでは元ネタ(https://arxiv.org/pdf/1701.02434.pdf)の4.2.1(p.30)に有るように質量マトリックスでコレに対応します。単純な話、Mが既知ならばLeapFrog書けるときにMをキャンセルしてあげて処理した後に、またMを書けて元々の物理量に戻してあげれば良いだけです。
ここで使ったMはqの分散行列そのものなので、warmup中のサンプリング結果から推定可能です。その補正を行うかのパラメータが以下のmetricです。
metric : str, {“unit_e”, “diag_e”, “dense_e”}
unit_eが補正なし、diag_eは各パラメータが独立と仮定し伸縮のみ、dense_eが回転縮小両方を見る。というものです。こうかくとdense_e一択に見えますが、dense_eにすると全てのパラメータ間の相関が十分い検証出来るぐらいに沢山のサンプリング数をwarmupに費やさないと、偶発的な偽相関(ノイズ)をひろって逆効果のMを推定してしまうかもしれません。
こんな長い文章ここまで読んだの?偉い!
したがって、パラメータ数が多い場合はパラメータ間相関を諦めてdiag_eに抑えておくというは十分ありな戦略です。また、事前に巨大データでMを推定して抑えてあるから、現場ではMは固定という事もあるでしょう。そういう時にunit_eが役立つと思います。(unit_eは使った事無いけど)
E-BFMIってなんぞ?
話の流れは一旦ブチ切れますが、時々みかけるE-BFMIの警告について見てみます。このエラーが出るときはmax_treeやadapt_delta(ステップサイズ)のエラーも出やすくて、解消すると一緒に消えてる事が多いので良く分からんけど消える奴な感じがするでしょう。
今回の実験では裾が重い部分布において発生します。非常に裾が重い(exp(|-x|**0.25)の例に関してサンプル数を増やして実験した結果が以下です。
ターゲットパラメータqのサンプリング結果を見ると左側の裾はサンプリング出来てるのに右側は全然サンプリング出来ていません。

これは不味い傾向です。左側に一度行ってしまえばそこをサンプルできるものの、そこと同じ確率であるべき右側は中々サンプルされないので、非常に長いサンプル数にしない限り偏りが出そうです。この偏りを直接的にみるための指標が皆がまずみるRhatなのですが、E-BFMIはそもそもこのモデルが病的にまで局所を取りやすい傾向にあるのかを調べます。やり方は単純です。H(q,p)で示される各サンプルのエネルギーE(n)を見ます。(n)はn番目のサンプルの意味です。
E-BFMIは元ネタ(https://arxiv.org/pdf/1701.02434.pdf)の6.1 (p.40)にあるようにE(n)-E(n-1)の分散とE(n)全体の分散の比です。
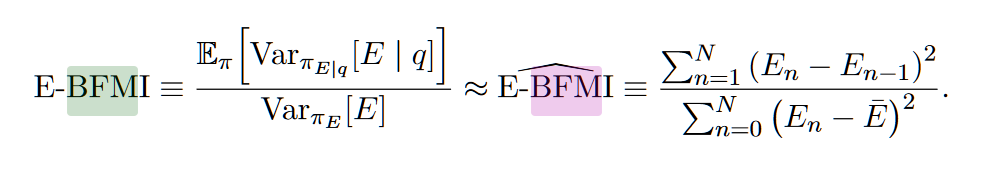
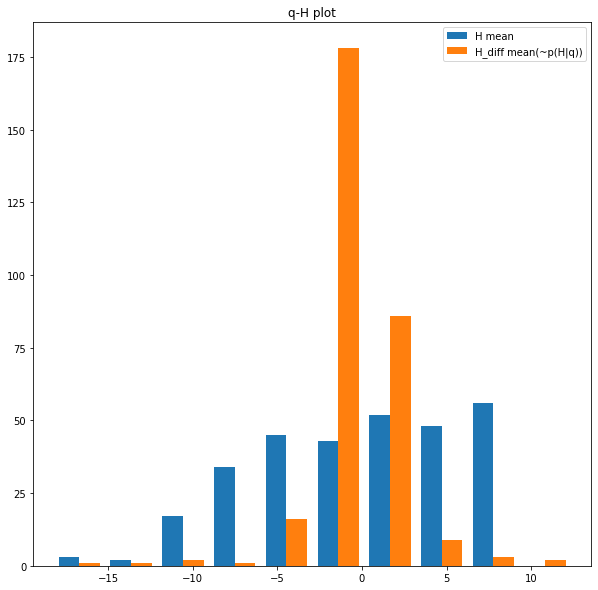
上は非常に重い裾での実験結果のヒストグラムである。なおB-EFMIは0.17であった。
H_mean:H(E)全体から平均値を引いたもの
H_diff: サンプル毎のH変動量(E(n)-E(n-1))
ヒストグラムをみると、サンプリングする度に得られる変動量に対して、最終的に全体の分布として得るべき変動量の幅が広く、例えばHを-15にするのは確率的にかなりの困難が伴う事が示されている。
ちなみにガウス分布の場合の同ヒストグラムは以下の通りで、E-BFMIは0.73であった。
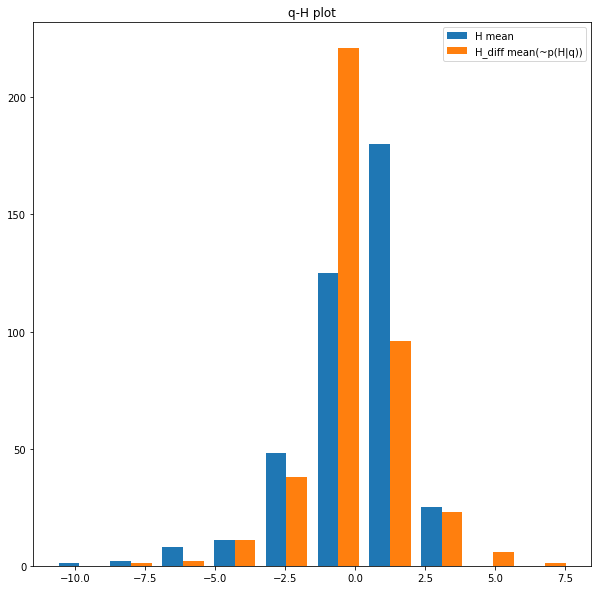
E-BFMIはある程度高い事が望ましいが、程度の問題ではあるが0.2~0.3を切ったら再パラメータ化等でモデルを見直して挙げないと、実用に耐えないとされています。
さいごに
簡単なHMCと単純なモデルを使った実験でわかる範囲でstanに出てくる良く分からんパラメータやら、謎の警告を解説してみました。論文なんかあたっても、具体例としてどう動くかがあまり書いてなくてイメージしづらい事が多いと思うので、2次元での可視化は解りやすくて良いかなと思っています。(自画自賛)まだまだ、解説しきれてない所どころか、私自身が理解してない所もstanなどのMCMC界隈には沢山ありますが。「使うだけなら簡単」なのでガンガンつかいましょう。自分が仕事で使いたいモデルでためして、RHatが1.0に近づかない時にようやく中身を知る必要でてきます。その時の一助になれば幸いです。
個人的にはパッと試してみて、RHatが1にならない時はプロジェクトそのものから手を引くのも一個人として正しい判断だと思います。RHatが1になるネタを見付ければいいのです。
