はじめに
ベイズ推定というと「スパムフィルタ?」とか、最近雑誌ニュートンで紹介されたノリで「AIを支える謎の技術」だとか「感染症の流行度合いの解析に使う」っていう風に紹介される事が多いと思います。
この一見、「はかって」、「信号を処理する」プログラムを書いている人からは縁遠い手法が実は凄く計測向きなので、簡単に紹介しようと思います。
ぶっちゃけF検定とかT検定とか非直感的な用語が並ぶ古典統計よりも「使うだけなら」簡単です。なお、ベイズ自体の入門には通称緑本「データ解析のための統計モデリング入門」がお勧めです。本文書では「計測」の側面で、特に回帰のみを雑に説明します。
説明につかった実装例はここに有ります⇒https://github.com/akirayou/stan_example/blob/master/regression.ipynb
計測におけるベイズ推定
ベイズ推定で推定するものは「真値の分布」です。例えば、ADCで読んだ値が2,3,2,3,5,1,…となっていたら真値はざっくり2.5位だけど2.1である可能性も2.9である可能性もあると考えますよね。つまり「確たる観測」が成された後から、「真値を推定する」のが計測です。ならばその確信度に応じて確率を求めて、真値の分布を計算できたら便利ですよね。特に95%信頼区間などを求めれば、「この範囲に95%ぐらいの確率で真値が入っている」と言う事が出来ます。
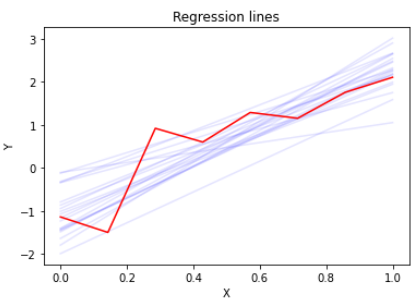
それを真正面からやるのがベイズ推定です。上の図の赤い折れ線は8点での計測結果を示しています。これに対して直線回帰をしたい場合、青線のように定規を沢山あててみて「これは当てはまってそう」という定規の当て方をピックアップします。そうして得られた定規の当て方が真値の分布そのものなのです。その行為自体は非常に直感的です。ここで「これは当てはまってそう」という基準が確率になります。
実際のベイズ推論では当てはまってそうな所だけ器用にサンプリングする手法を使ったり、離散的な当て嵌め行為を連続な分布関数で記述したりしていますが、stan等の推論ソフトがやってくれるので気にする必要はありません。(うまく推論できないという、問題にぶち当たるまでは)
まずは、重さでも量ろう
一番単純な推定、ガウス分布を仮定して計測値の真値を求めてみましょう。データは以下のヒストグラムの通り、平均0で標準偏差1の乱数から作った20個の乱数です。
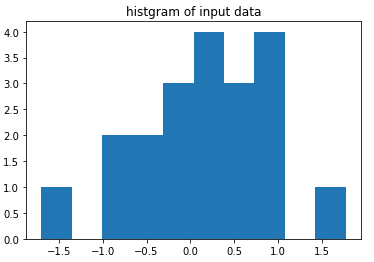
最尤推定でやるならば、平均値を求める事だという事は何となく覚えているでしょう。推論はpythonからstanを呼び出して行います(実行結果はこちら)。stanのコードは読むのにコツがいるのですが、重要な部分はmodel部分です。
2 data{
3 int N;
4 vector[N] Y;
5
6 real mu_u;
7 real mu_s;
8
9 real sigma_u;
10 real sigma_s;
11 }
12
13 parameters{
14 real mu;
15 real<lower=0> sigma;
16 }
17 model{
18 mu ~ normal(mu_u,mu_s);
19 sigma ~ normal(sigma_u,sigma_s);
20 Y ~ normal(mu,sigma);
21 }stanの詳しい書き方は説明しませんが、Y~normal(mu,sigma)という部分が平均mu,標準偏差sigmaのnormal(正規分布)からサンプリングして、観測データYに当て嵌めいるとうモデルを使う事を意味しています。まさに本体の部分で尤度関数等と呼ばれます。「mu~」「sigma~ 」の部分は事前分布と呼ばれるものです。パラメータは十把一絡げにθで示して、尤度関数を「とあるパラメータθの時の確率p(Y|θ)」で示して、事前分ぷを「p(θ)」で示した時の、p(Y|θ)p(θ)これは、すなわちベイズの定理を使って「Yを観測した時のθの確率p(θ|Y)」を計算しています。この確率を用いて、真値(=パラメータ)の分布を求めています。
事前分布「mu~」の部分や「sigma~」の部分を省略すると、θの値が何であっても何も掛けていない(=1を掛けている)事になるので、十分に広い一様分布を事前分布に設定したのと同じになります。
事前分布について
計測の場合事前分布の設定しだいで大きく結果が変わるようなトリッキーなモデルはそもそもあまり使わないので、事前分布は深く悩むことはないと思います。妥当な裏付けや、特定の仮定があればかっちり設定するけど、それ以外では設定しないか、広く設定する(=弱事前分布)というのが多いと思います。
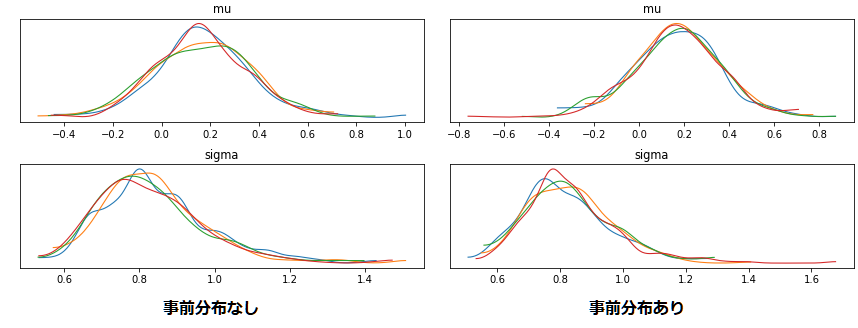
上の図は事前分布有無での結果の違いを示しています。mu~Normal(1,3), sigma~Normal(0,3) とそこそこ絞っていますが結果に大きな影響はないです。
もちろん、例えば計測器のノイズ振幅が事前の校正によって解っている場合等はかっちりとした事前分布を与えることで、パラメータmuの信頼区間をより狭めるという使い方も有り得ます。事前分布は真の分布をゆがめると言う人もいますが、それを言うとモデル関数自体が現実を歪める元凶なのでどっこいどっこいです。「一定値である」と仮定するのと同じぐらいの「モデル設計諸元」にすぎません。(どのモデルが良いかはWAICやWBIC等で比較しますが、最後は人間に対する納得性が求められたりしますよね・・・)
弱事前分布の使いどころ
上の例で弱事前分布が大した影響を与えない事を示しましたが、それを使う理由を実例で説明したいと思います。問題を一気に複雑にして、ガウス関数へのフィッティングを行います。(実行結果はこちらの「ガウス関数フィッティングの例」)
最初の定規の例で示したように、フィッティングした関数を青線で示しています。
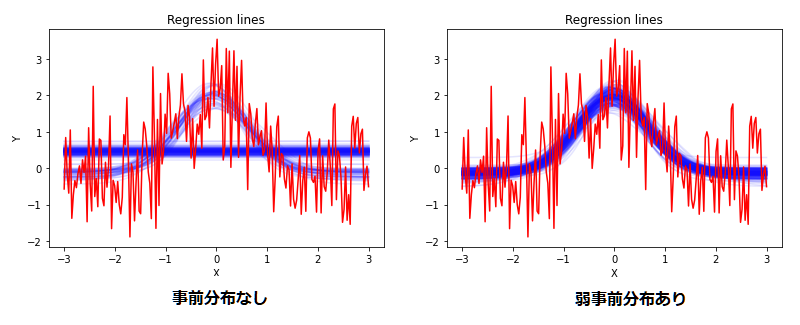
事前分布のない場合はガウス関数を推定する時もあれば直線になってしまう場合もあります。これはサンプリングによるベイズ推定の限界のが原因です。以下は事前分布なしの場合の算出されたパラメータ分布です。
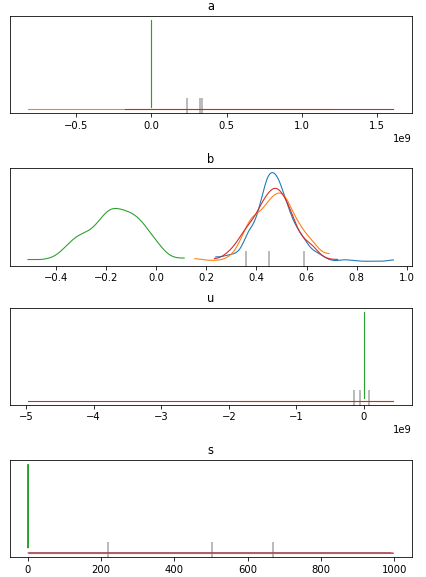
ピーク関数のパラメータa,u,sが非常に大きな値をとる場合がある事を示してます。ピーク形状はある程度重なっていれば尤度を計算して意味がある値がでますが、かけ離れたピーク同士がどの程度重なっているかを計算してもノイズしかでてきません。そのために、局所解的なものに陥ってまともにサンプリングされません。弱事前分布にはこのような状態から脱出するための制約としての役割が有ります。
推定失敗の判断
上のように回帰結果のグラフをみれば、推定こけてるのはわかるのですがstanの結果サマリーからも失敗を読み取れます
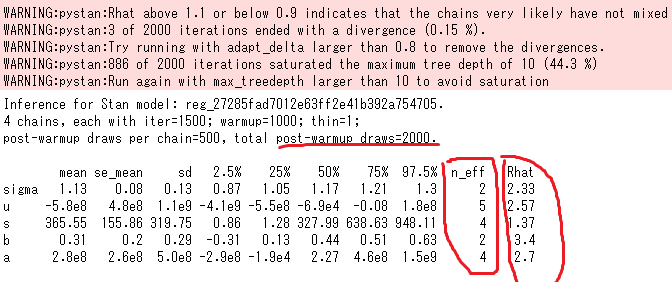
一つにはWARINGが出てることで、怪しい時はでてきます。次に必ず見る必要があるのはRhatです。WARINGにかいてあるように1.1こえると、サンプリングが局所解にトラップされてる可能性を示しています。さらにn_effがpost-warmup draws=2000に比べて非常に小さいです。これが1/10もない状況だとサンプリングそもそもうまくいかないやっかいな問題を解いている事を示しています。例えば今回のように尤度の微分がゼロになって消えたり、逆に急激に大きくなる点がある。運がよければstanのsamplingのiter数(warmup数)を増やせば解決する事もありますが、n_effが極端に小さい時はそれすら期待できません。弱事前分布を含めたモデル設計の再検討が必要とされています。
弱事前分布でもうまく行かないときは、根本的にモデルを検討しなおす以外に再パラメータ化というテクニックもあるのですが、これはまた別の機会に。
線形回帰の例
それでは、一番使う回数が多いと思われる線形回帰(ax+b)の例を見てみましょう。(実行例「線形回帰の例」)今回の例程度の回帰では事前分布なしでもいけます。
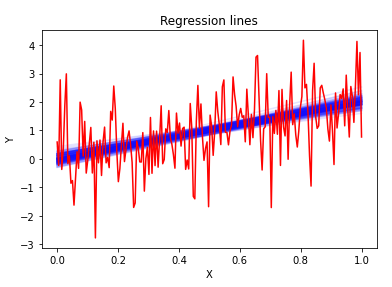
古典的な手法で、標準誤差を算出する要領でも算出できるのですが、難しい事を考えずに以下のstanソースコードのように直接回帰式を書くだけ真値分布を見る事ができています。個人的には、ここが最大のメリットだと思っています。サンプリング不能に陥らない限り、使うのは超簡単なのです。以下はstanコードの例です。
2 functions{
3 vector func(vector x,real a,real b,real sigma){
4 return a*x + b;
5 }
6 }
7 data{
8 int N;
9 vector[N] X;
10 vector[N] Y;
11
12
13
14 }
15
16 parameters{
17 real a;
18 real b;
19 real<lower=0> sigma;
20 }
21 transformed parameters{
22 vector[N] yy;
23 yy=func(X,a,b,sigma);
24 }
25
26 model{
27 Y ~ normal(yy,sigma);
28 }回帰関数はfunctionブロックにある、funcで定義されています。線形式以外にするにはパラメータの宣言周りの他にはfunc関数の中身を弄るだけで様々なモデルを試せます。これを直接使うのはtransformed parameters ブロックです。ここで一旦yyにという変数に真値推定値を入れてから、誤差成分normal(yy,sigma)として加味しています。一旦パラメータyyとしてパラメータ変換している理由は今回の場合はパラメータとして宣言しておくとサンプリングして後から参照できるというのを使って各計算結果を記録するためであって、計算上の深い意味はありません。(python側のplot_rec関数でyyを参照して青い線をプロットしている)
Y ~ normal(func(X,a,b,sigma),sigma);なので上のように直接model部分に関数を書いても、ほぼ同じようにサンプリングできます。なおtransformed paramtersは再パラメータ化というテクニックに使いマス。具体的には∂p(Y|θ)/∂θ が複数のパラメータが絡んだ急激な変化を伴う場合にうまくサンプリングできない場合があります。このときにθに変換関数をかませてこの問題を解決します。(nealの漏斗の例がstanのユーザガイドにのってます)
stanプログラミングの工夫
stanのプログラミングにあたって、stan_util.pyにあるような自作ヘルパ関数を使っています。機能は2つで、
- 毎回コンパイルするのは効率がわるいので、コンパイル済みのオブジェクトをキャッシュ
- テンプレートエンジンmakoを使って必要な部分を追記
1つめはstanプログラマには必須の機能なんですが、本家で実装されるのは次ぎの世代のpystanからだそうです。(pystan-nextで検索)
テンプレートエンジンmakoを使っているので、回帰のプログラムはstanのコードを直接いじることなく色々ためせます。簡単なので改造してみてください。
param=[{"name":"a","prio":"none","opt":""},
{"name":"b","prio":"none","opt":""},
{"name":"sigma","prio":"none","opt":"<lower=0>"},
]
d={"param":param,"func":"return a*x + b;"} #ここでモデル関数パラメータはparamの所に宣言してprioがnoneなら事前分布なし、normalなら正規分布になります。事前分布を指定するときは対応してstan_dataに平均「[パラメータ名]_u」標準偏差「[パラメータ名]_s」も指定してあげる必要があります。optはパラメータ宣言時のupper/lower設定用です。 回帰関数はstanコードのfuncの中身そのものです。
今後
勢いで書いたので舌足らず感があるので追記したい。階層モデルは説明したい(3ロットで実験した結果のとりまとめとか)。再パラメータ化もできれば。
ただ、飽きなければだけど・・・。