ScipyのODEソルバーというとodeintがよく解説記事に出てきますが、マニュアルを読むと「Old API」と書いてあるんですね。新APIのほうが柔軟性があります。
- 発散orNaN落ちしちゃうけど、その直前まで見たい。
- 特定の条件の時だけ時間分解能を高く計算結果を見たい。
という時には特に新APIのほうがお勧めです。ということで使い方簡単に説明します。
Solverを選ぶ

マニュアルページをみると6つほどソルバーがあります。何も考えたくない人はLSODAを選べばOKです。微分方程式のモデルの良さ自体を検討したい人や他の処理系との互換性を気にする人はそれ以外を選びましょう。例えばstanはRK45かBDFしかありません。
微分方程式を関数に落とす
これはodeintとほぼ同じですが、設計方法簡単に説明します。以下の例はLCR直列回路です。変数が入った配列yを受け取り、それを時間tで微分した配列をreturnで返します。odeintとの違いは引数の順番だけなので、odeintを使った事があるひとは飛ばしてOK.

入力と出力は単純で解りやすいのですが、一般的な偏微方程式から書き換えが必要です。電源Pの電圧・電流をPv,Piという風に以下添え字で書きます。LCRに電源Pを繋いだ時の偏微分方程式は以下のようになります。
Pv=Lv+Cv+Rv
Rv=Pi*R
dCv/dt=C * Pi
Lv=L * dPv/dt コードに落とす時は、まずdPv/dt,dCv/dtの項を移項して左辺に整理してあげます(上のpythonコードの最後3行です)。そこに必要な各変数(Lv,Rv等)を計算してあげるのですが、ここで使えるのは「定数」とreturnする偏微分に対応する入力値(Pv,Cv)のみです。なおPvは本来はtで与えられる関数ですが、Pv=sin(t)を突っ込むと誤差がガンガンのるので注意が必要です。ここではPvとPvcの二変数に一旦わけて、グルグル回って貰ってsin波を生成してます。時間tはt倍するとか1/t倍するとか、step応答を見てみたいとかぐらいにしか使えない子です。
ODEを実行
実行するためのソースは以下のようになります。

LSODA関数を呼ぶとオブジェクト(ode)が帰ってきます。このオブジェクトが持つstep()関数を繰り返し実行するだけです。このときode.statusがrunningである間実行すれば目標とする回数実行できます。このときodeは以下のメンバを持ちます。
- ode.t : 現在の時刻
- ode.t_old: 前回のstepで実行した時刻
- ode.y: 現在の変数y
普通はode.tとode.yの値を配列などに入力して記録すればおおよその形が解ります。このループの中でyの値が大きくなりすぎたらbreakするという処理をしてあげれば発散直前まで計算するという使い方が出来るようになります。
また、step毎に実行される時間間隔は計算精度が保てる限り長くして効率良くサンプリングするようになっています。このためデータ点が少なすぎて困る場合もあるでしょう。そういう時はode.dense_output()を呼べば、補完関数を生成してくれますので、必要な時間分解能分だけyを補完して求められます。
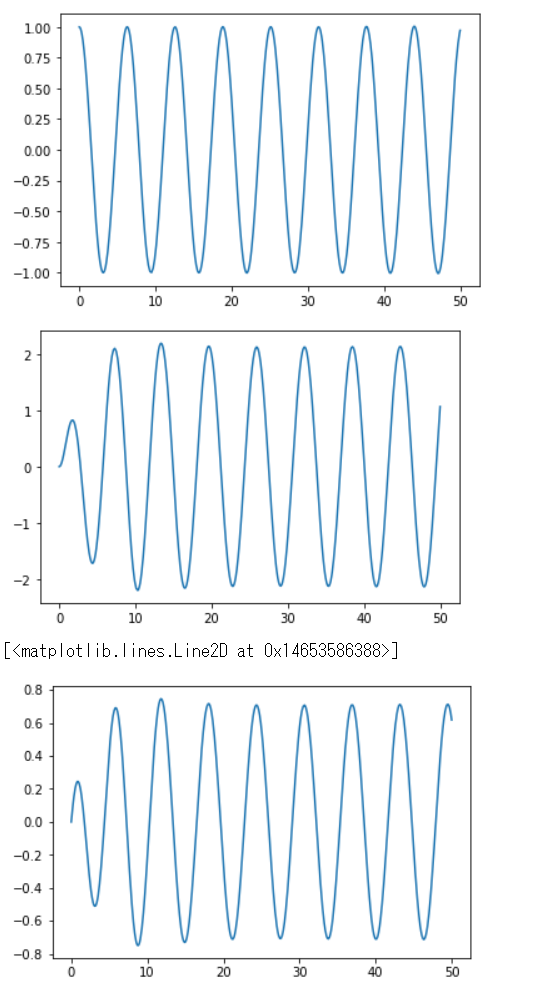
実行結果のPv,Cv,Piは以下のようになります。普通ですね。
ソース
https://gist.github.com/akirayou/2a294658eaef1a337911696bf35ae985#file-untitled1-ipynb