計測関連だと混合ピークって良く使いますよね。頑張ってハイパスフィルタ通して各ピークの位置を求めてみたり、モデル関数フィッティングで頑張ってみたり。それ、ベイズ推定でやりたいですよね。ってのが今回の例題。
そこでノイズが有る時はうまくいってたのに、ノイズが減るとstan(やpyMC等HMCベース)での推定がうまく行かなくなるという、一見直感に反する現象があるので紹介します。
ノイズだけでなく、データのサンプリング速度が速く、密に取るほどコケるというコレもまた、なんで情報増えてるのにコケるねん。って突っ込みたくなる現象も起きます。
例題:ガウス関数2ピークの回帰
以下の赤と青のガウス関数を足し合わせた信号にさらにガウスノイズがものがターゲットです。詳しい実装はhttps://github.com/akirayou/stan_example/blob/master/two_gauss.ipynbを見て下さい。
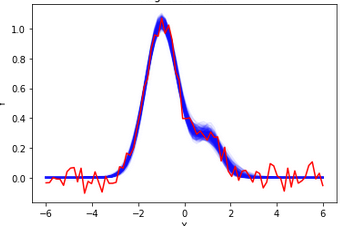
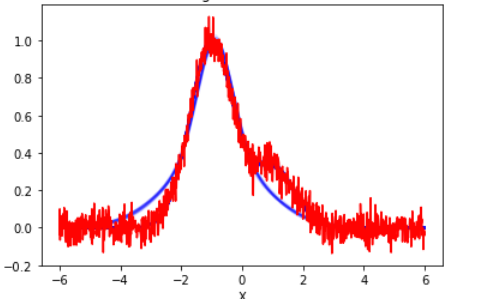
例えば以下のグラフの赤い線が観測データです(データ点数N=80,ノイズσ=0.05)。
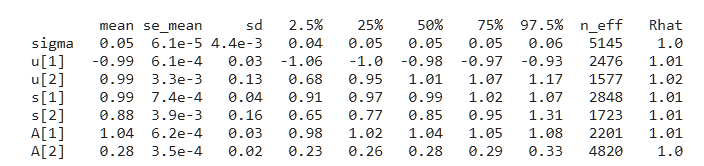
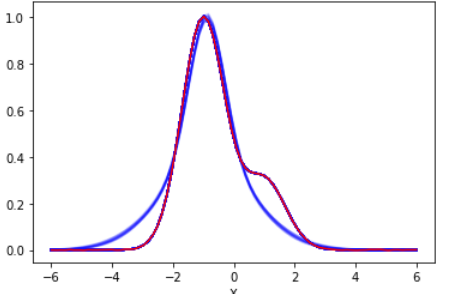
青い線はstanでサンプリングした結果を重ね書きしたものです。見た感じ自然な分布を獲得出来ています。Rhatも1.02に納まっています。
後で、コケてるサンプルと比較するために、比較的旨く行っているこのサンプルのトレースプロットも見てみましょう。左にあるグラフにある複数の色の線は各chainでの各変数の事後分布を示しています。通常は概ね一致する分布をとります。
ノイズを減らしてみよう!そして死。
ノイズをσ=0.05から0.001に減らしてみます。
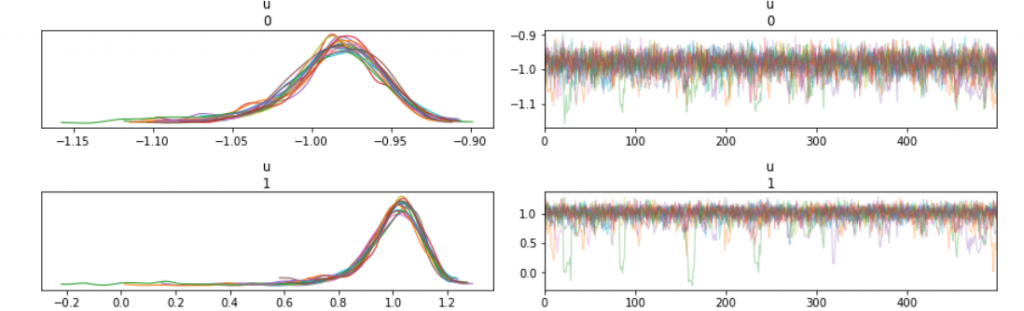
サンプリング結果は概ね、観測データである赤い線に沿って欲しいのに全然違う所を通っているサンプルがいます。トレースプロットをみると、chainが2つの派閥に分かれているのが解ります。
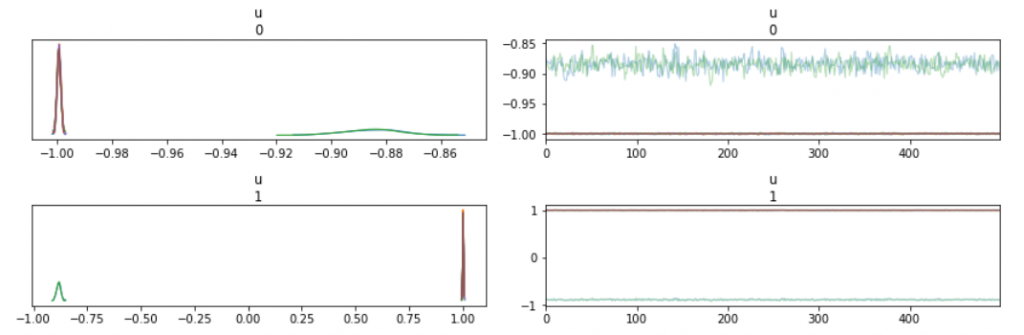
これは、MCMCサンプリングの開始点の運が悪いと、局所に捉えられてしまっているんですね。
これが起きる原因は直接的にはMCMCが死の谷を超えられないという所にあります。死の谷は確率がほぼゼロ地帯のことです。以下の@teramonagisさんのスライドで詳しく説明されています。
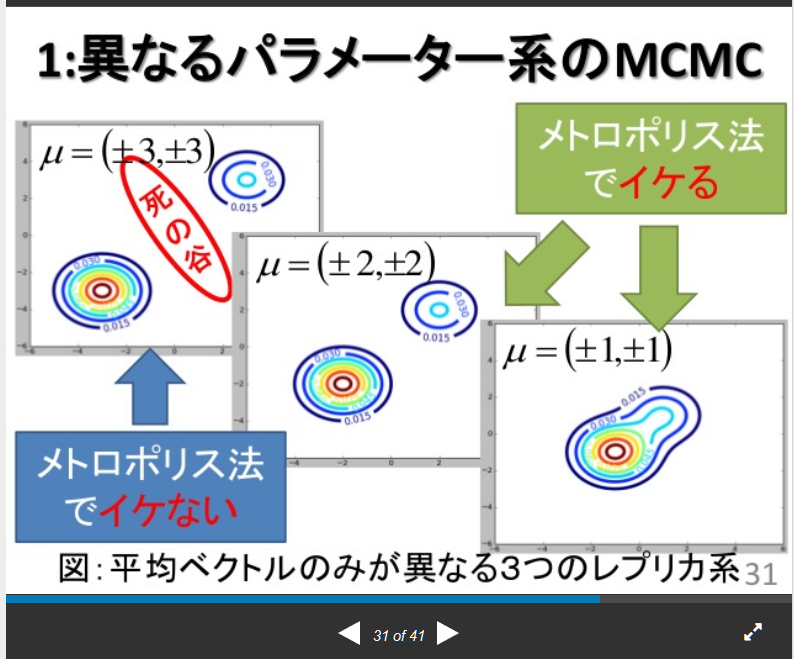
死の谷が発生する理由ですが、ガウス関数のパラメータを連続的に変えていくと、二乗誤差が単調に大きくなるのではなく大きくなったり、小さくなったりしながら変化するためです。そのせいでノイズ幅を示すσに比べて局所解の谷が深い場合にMCMCのサンプリングが脱出出来なくなってしまいます。
実はこの問題勾配法で最小二乗値を求める時にも起きるので、ベイズ特有の問題ではないのですが・・・ベイズでやってると効率良く局所解を見付けてくれるので目立ちます。
データ点数を増やしてみよう!そして死。
ノイズ量はそのままに、データ点数を増やしてみましょう。情報は増えますね。情報増えただけだから・・って期待させておいて、死にます。
トレースプロットの形状は若干違うものもの、局所解にトラップされてるのが見えます。
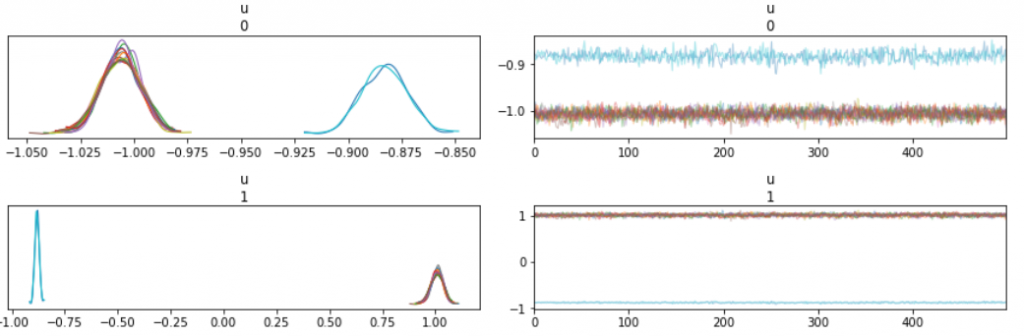
情報が増えるとガウス関数が旨くフィットしているかどうかの尤度がより鋭敏になる、すなわち局所解の谷が深くなるので死にます。
解決方法:2段階焼き鈍し
解決方法として今回は焼き鈍しをやってみます。まずその前に温度って何だ?という話になります。MCMCサンプリングの時は尤度p(x|θ)をβ乗する事があります。このβは通常1ですが、βを0.1等小さな値にすると分布をよりぼかす事が出来ます。このβを逆温度と呼びます。(実は私もそんなに詳しくは知らない)
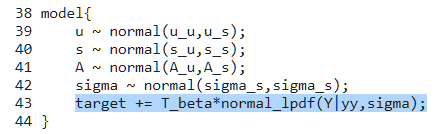
stanのコードでは上の水色で色をぬった部分が逆温度を適用する部分です。targetは事後確率を対数とって符号を反転させたものです。normal_lpdfは正規分布の対数の負なので((Y-yy)/sigma)**2をサンプルの数だけ加算してるんですね。データ点数が増えれば谷はより深くなるし、ノイズ幅であるsigmaが小さくなっても谷がより深くなるのは直感的にもよく解るでしょう。T_betaはコレを単純に0.1等小さな値を掛けることで対処していると言えます。当然ながらその分得られる事後分布は元々計算しようとしていたモノよりもブロードな分布になります。
このように高温(βが小さい)条件でえられた結果を流用して、局所解ではない範囲を選んで定温(β=1)条件で改めてサンプリングするのが焼き鈍しです。通常は徐々に冷却するのですが、この程度なら2段階で十分逃げれます。
実装はとても簡単で、βを小さい値下の例は0.001で実行した後に、常温のサンプリングの初期値として前回の実行結果の最終位置(ガウス関数等のパラメータ)を初期値にするだけです。pystanではget_last_positionで最終位置を取ってこれるのですが、古いpystanにはないので、新しいpystanにバージョンアップしましょう。

ノイズを減らした場合での焼き鈍し結果
β=0.001でまずは推定します。
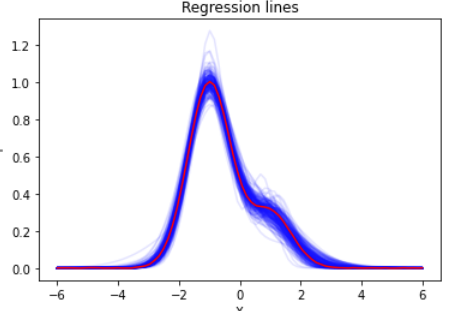
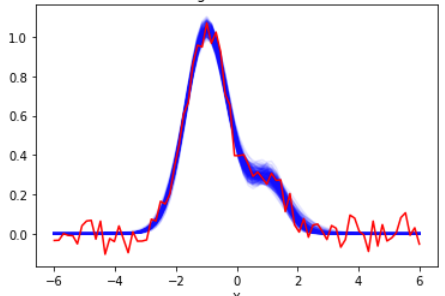
青い線で示される推定結果がかなりブロードになっていますが、自然な広がり方に納まっているのが見て取れます。このサンプリングが16chainで行われているので、最終いちは16個あります。この16個をそのまま引き継いでβ=1で実行すると綺麗に推定できるのが見て取れます。Rhatも1.0でバッチリです。
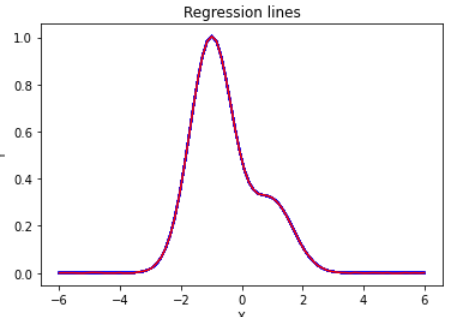
データ点数を増やした場合での焼き鈍し
データ点数を増やしたときは試行錯誤の結果β=0.1にしました。
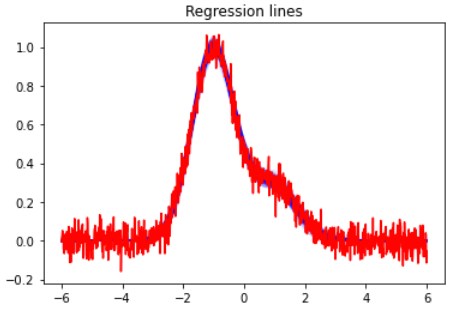
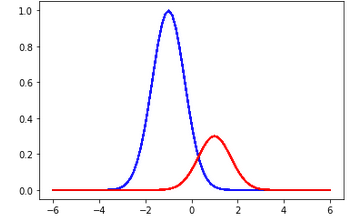
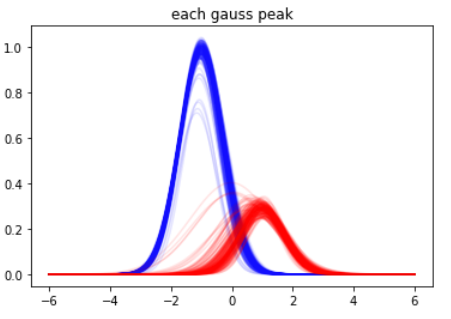
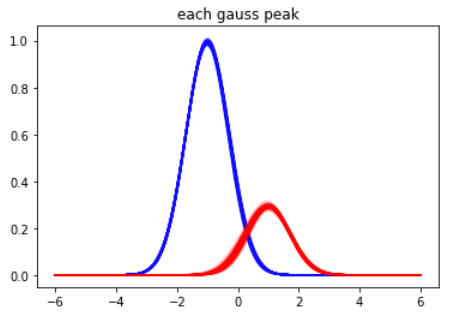
β=0.1程度なので、推定結果の分布はそんなに拡がりません。見易くするために、二つのガウスピークをそれぞれ青・赤にわけてプロットしたのが以下です。そこそこの幅はあるものの、わりと自然な範囲で落ち着いています。
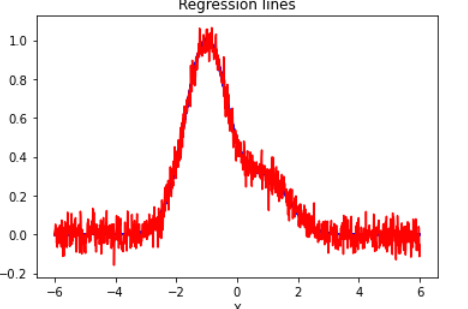
この結果を引き継いで、定温にしたのが以下です。ノイズに比べ推定幅のほうが小さいので完全にみえなくなっています。Rhatは1.0になっていてバッチリサンプリングできています。
分離した図を見ても妥当そうです。
焼き鈍しは完璧か?
上の例では局所解と大域解があるという形だったので、焼き鈍しでOKでした。しかし現実には、パターンAとパターンBが五分五分で有り得るというリスクを見出したい場合があります。このような時に焼き鈍しを使うと五分五分のリスクを見逃すかもしれません。例えばchain数が4の場合、2/2**4=1/8の確率で全員がパターンAorBを選んでしまうかもしれません。
五分五分のリスクを見付けた時はエラーになればいいやと言う時は、chain数を十分に増やしておけばOKですが、両方をちゃんとサンプリングしたいという場合にはレプリカ交換法(パラレルテンパリング)を使う必要があります。(計算量めっちゃかかる)
むしろ私が教えて欲しい事
高温条件のβは目視で試行錯誤するのは簡単です。ただ、実際には現場で良く分からないデータを突っ込まれるわけなので、自動化したいのですが自動的によさげなβを決める方法はガウスピーク信号にターゲットを絞ったとしても妙案はないです。
そして、そもそもガウスピークが正規分布ノイズ(二乗誤差)に対して局所解もつような構造なのが悪いんじゃん。ガウス関数のモデルもしくは、二乗誤差のモデルの方を改良して局所解モードの時は緩く評価するような旨いモデルを作れば良いんじゃないの?という話もあります。
このへんは、色々考えはしてるものの妙案が浮かばないので誰か知ってたら@akira_youまで教えて貰えると嬉しいです。