計測での分解能が足りないから、信号処理やAIでなんとかしてみました。良くある研究ですね。適用分野さえ違えば新規性が出るので、学部の卒論に最適です。(私も顕微画像の超解像でした)
ただ実用的な研究と「やってみた」の間には、今日も冷たい雨が降っているのが現実です。「やってみた」は重要なので否定はしません。ただその先に待ち構える地獄を知った上で、その薄氷を踏み抜かないように逃げ切りましょう。ということで、ざっとこの辺知っとくといいよーな話を列挙していきます。
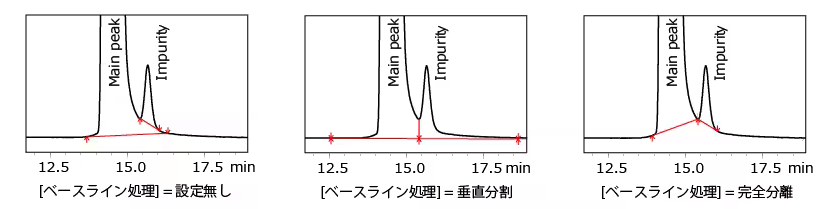
ピークデコンボリューション(Deconvolution)
化学分析分野では「ピーク分離(separation)」というと化学的・物理的手段でピークを分離する事を指すので、この単語は使えません。なので歴史的にピークデコンボリューション(Deconvolution:逆重畳)という単語を使います。ピーク形状をボケ関数とみなして、フーリエ空間で除算するあれです。現在では使う人いないので、はっきりいって誤用です。私は「ピーク分離アルゴリズム」と呼ぶか「ピーク分解(Decomposition)」と読んでいますが、分析化学者の前では日和ってデコンボリューションと呼んでいます。
ピーク「デコンボリューション」を使っている特許例(https://patents.google.com/patent/JP3025145B2/ja)を一つあげます。デコンボリューションの問題点は分離度を上げるために高周波強調をすると、その分ノイズがガンガン載ることです。上の特許の場合は複数波長のデータをかき集めてSN改善してから処理するとか、涙ぐましい事をしてます。定量用途にはぶっちゃけ向きません。ノイズの中からピークトップの位置だけ読めれば良い!という割り切りなら良い手法です。
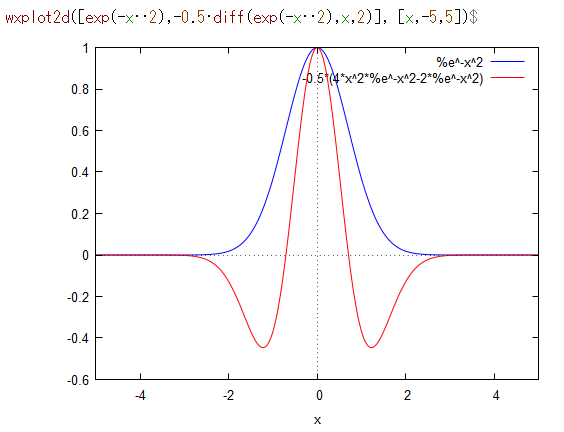
2次微分による方法
他の信号に埋もれてるピーク検出したい場合ぐらいにしか使えない手法ですが、通常のピークよりも2次微分のほうが高周波で有る事から夢を見る人もいるのですが、ピーク分離に使おうとするとデコンボリューションと変わりないです。ちなみに、分析化学信号処理界隈ではみんなサビツキーゴーレイフィルタ(平滑化2次微分)大好きです。
モデル関数フィッティング(最小二乗)
吸光スペクトル分布だったらVogit関数だとか、理想的なクロマト関数ならEMG関数だとかいろんなモデル関数があるので、それをフィッティングしてあげようというものです。ガウス関数みたいに波形の自由度が低い関数ならば一意に解が求まるが系統誤差が大きい。逆に様々なテーリング形状まで細かく表現できる関数を使えば系統誤差はなくなるが、解が一意に求まらず変な解を示す。といった問題があります。研究の途中であたりを付けるのには有用ですが、検証は別途という感じ使う程度じゃないでしょうか?
一言でピーク関数といっても、沢山種類があるので眺めてて楽しいです。例:https://www.lightstone.co.jp/origin/flist6.html
多次元検出器をつかっての因子分解(SVD/NMF)
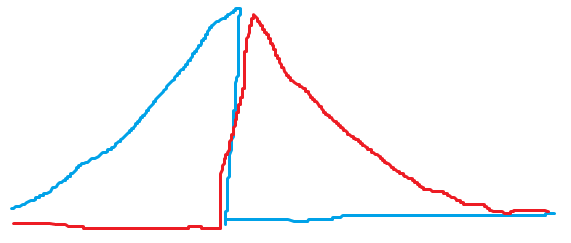
クロマトでピーク分離するんだけど、検出器に分光スペクトルなどの多次元検出器を使う場合があります。その場合、下図のように各物質は固有のスペクトルをもつので、特異値分解(SVD)や非負行列分解(NMF)で分解できるはず!という夢を一度は見ます。シンプルで美しいですしね。
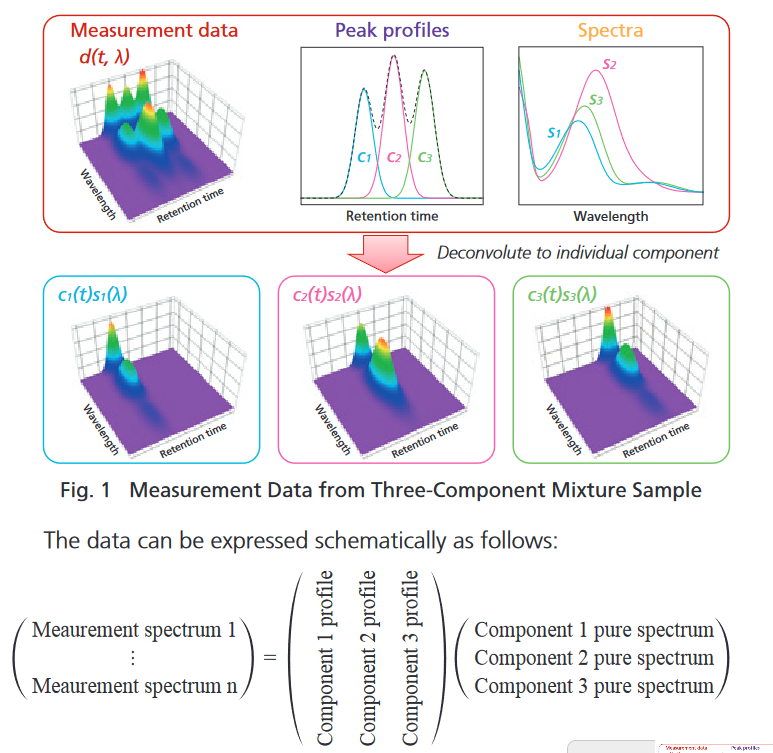
C1とC2のようにほぼC1のみの純スペクトルが解るよ!というようなデータでは、うまく行って実用的に使えます。しかし、例えばクロマト信号の分離でそんな状況のときは、垂直分割でかなり良い精度が出ちゃうので、意義を問われてしまいます。使うとしたら、ピークテーリング形状になんらか物理的な意味があって、それを読み解きたい系だと思います。
上の図のように元の信号強度差が大きく、片一方のピークの上に完全乗っちゃってる時は、載っているピークの分解結果は、解が一定の範囲(range of feasible solution)を持つので、因子分解結果はその解のうちの一つを示しているのに過ぎない事に注意が必要です。そのときの偶然のったノイズと因子分解アルゴリズムに与える初期値に引っ張られて解が求まります。
あとピークの分割数を見誤ったり、分解アルゴリズムにあたえる初期値が悪かったりすると下図のように、一つのピークを2つに割ってみたり、逆に無理矢理1つにまとめてみたりと、お茶目な結果を出したりもします。
MCR系
MCR-ALSといえばRoma Tauler先生でしょうという感じの分野ですね。因子分解の問題点は最小二乗となる解が沢山あることなので、「スペクトルは正値」「クロマトは単峰性」といった制約を追加しましょう。というのがクロマトに最初(?)に適用されたMCR系アルゴリズムであるMCR-ALSです。だいぶ昔からやられてるようですが、ぱっとぐぐってpdfみつかるのはこれでした。
制約を追加することで、解の範囲は狭まるのですがそれでも解に範囲は有ります。その解範囲を調べようというMCR-BANDS等の方法があります。
余談:研究対象するならLC-PDA?LC-MS?
Taular先生はLC-MSなどの質量分析装置を検出器として使うクロマトで説明する事も多いです。分光器のスペクトルは物質がちがうとスペクトル形状が違うものの200-350nm波長帯では必ず信号がでます。一方でMSでは物質Aはとある質量値(m/z)で信号が出るが、物質Bは全く信号が出ないという事があります。ぶっちゃけ運とSNがよけれNMFで解けます。MCR-ALSはNMFのもつ「スペクトルは正値」という制約に加えて「単峰性」を足してるので、MSの問題を良く解けるでしょう。という事だとは思います。しかし、装置のダイナミックレンジでいえば分光器のほうが高いので、分光器とMSどっちが良いかは計る対象によります。
PALAFAC系
MCR-ALS系をやってると必ず一緒にでてくるのですが、理屈としては複数装置でみてあげれば良いよね。というだけです。行列からテンソルに拡張されるだけといえばそれだけなのですが、ノイズモデルやリニアリティが違うものを混ぜて扱う難しさはあると思います。ただ、私はあまりさわってないので今回は紹介省略。
MCR系+モデル関数制限
MCRでは多くの場合、非負や単峰制限といった比較的単純な制約しかいれません。一つのアルゴリズムで多くの測定系に適用するという事を考えれば真っ当な判断だと思います。そこの上にのっかって、「特定の物質の測定にしか使わないので、クロマトはEMG関数で十分近似できる。」という風に分野特化型で性能を上げるのがモデル関数を使うタイプのMCRです。モデル関数の近似精度は十二分にあるのか?という議論が常につきまといますが、がっつり解の範囲を削れる手法になっています。
例:https://www.sciencedirect.com/science/article/abs/pii/S0021967316312535
誤差の解析はMCR-BANDSだけでよいのか?
MCR-BANDSの基本アプローチは二乗誤差=0の平原が拡がっているので、その範囲を求めるというものです。実際には偶然誤差のせいで凸凹していたり、系統誤差のために二乗誤差=0とならずにオフセットがのったりしています。なので適当なマージンを求めて、解の範囲を求めています。それを効率よく解く方法として、成分間で観測データの割り振りの比率を変える行為を行列の回転として表現してたりします。なので例えば、SNが悪い信号の分離を行う際に「誤差の伝搬」までは考慮されてなかったり、そもそも誤差として無視する幅の設定の妥当性という意味で境界部分が怪しいといえば怪しいです。
MCR系+モデルう関数のように、関数フィッティングだと考えるとFIM(フィッシャー情報行列)を使って回帰パラメータの分散を求めよう!という発想になるかもしれません。FIMは回帰パラメータへの誤差伝搬を多変数の複雑な式でも使える用に一般化したものと思っとけばOKです。しかしながらFIMは解の範囲がある=尤度が台地を描く場合には通常使えない事が知られています。https://www.jstage.jst.go.jp/article/jnns/10/4/10_4_211/_pdf
なので上のURLの解説通り、計算量が沢山必要で有る事を覚悟して、ベイズ推論(MCMC)すればいいよね。ということで最近のパソコンをゴリゴリこき使う方が取られています。https://doi.org/10.1016/j.chroma.2023.464136
理論上は正しいですが、MCMCは特異モデルを正しくあつかうかもしれませんが、特異モデルぶつかると尤度が平坦な部分と、急峻な所がまざって曲率(curvature)変化が凄くなってサンプリングが難しくなるという問題があります。https://browse.arxiv.org/pdf/1701.02434.pdf
この問題の面白い所は「曲率の変化」が重要なので、例えばノイズのないシミュレーションで作った綺麗な混合クロマトピークは綺麗に二乗誤差=0のフラットな領域を持つのでMCMCをつかったMCR系のピーク分離をすると全くもって有効なサンプリングができなくなります。ノイズを付与してあげると要約MCMCがまともに走ります。最小二乗法の時のアルゴリズムテストの時はクリーン信号から普通は始めるので理屈を知らないとキツネに騙され気分になります。
アルゴリズムの評価の際にはシミュレーションで評価して、実データで実証するという形が多いですが、ノイズだとか細かい所にまで気をつける必要があります。
小ネタ:そもそもそのノイズ正規分布ですか?
計測機のノイズを雑に正規分布としたモデル化多いですよね。その前提が崩れるとベイズ推論(MCMC)が一発で死にます。例えば多くのクロマト検出器はノイズが時間方向に相関を持っていて独立ではないです(光学的に・電気的にローパスかかっちゃう)。MS検出器は時間相関もたないけど、ポアソン分布っぽい挙動を見せたりします。
また市販製品をつかって研究する場合、内部的にどんなローパスかかってるかだとか、データ圧縮のために小さいデータ足切りしてるとか、装置メーカーのしかも秘伝のタレにつけこまれたファームウェア知ってるような担当者にチマチマ聴かないと厳密なモデル化は難しかったりするので、そこをうまく逃げるモデルだとか、研究方針を立てないと簡単に地獄に落ちます。
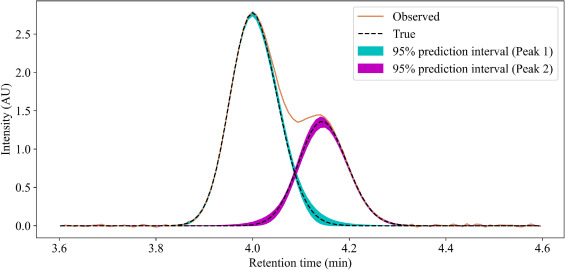
ピーク分離後の誤差(信頼区間)までやったぞ、それで完璧?
と言いたいところですが、上の議論は観測データから真値を推定する「計算処理」にどれだけの誤差が見込めるかを見ただけです。実際の実験にはそもそもの試料調合だとかの計り取り誤差やオートサンプラなどの装置の再現性自体の問題があります。
実際の検証にあたっては、それらを分けて議論できる実験プロトコルを考えないと評価で詰みます。分析計測アルゴリズムの開発って、「計測装置そのもの」がテーマなので、信号処理のせいなのか?そもそものデータのせいなのか?見極めるのがすんごく難しいです。
さいごに
計測信号がちょっと混ざってるのを何とかソフトウェアで頑張りたいという最後の一手としてのピーク分離アルゴリズムの例をMCR系の技術を中心に紹介しました。
ピーク分離界隈ではソフトの限界が認知されて、じゃぁ限界があるとして、どう運用するの?というフェーズに入ってると思います。そこで誤差(信頼区間)について安直に考えればベイズ推論(MCMC)だよね。という事を紹介しました。
私個人としてはMCMCに必要なCPUパワーや実装するためのフレームワークも含めて基本的な道具は揃いつつあるな印象です。これからは、ここに適用したら効果的やん!というのを単に最小二乗でモデル化して代表例を示すだけじゃなくて、今持っている観測データ群から将来期待される誤差を含めて議論する時代に入ると思います。もちろん統計や情報学ガチ勢から見れば「今頃?」という感じかもしれないですが、計測データの信号処理分野って若干ゆっくりなんだと思います。