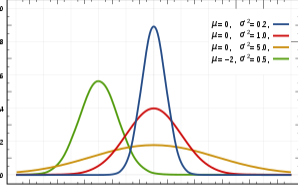
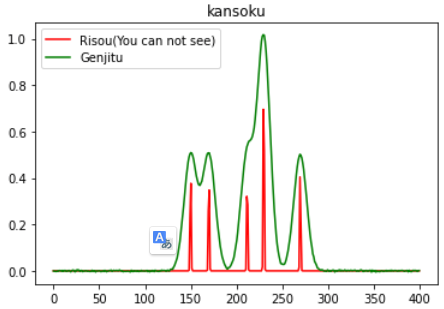
なんかのエコー信号だったり、分析装置系のデータだったり、上の図みたいな信号使う事あるよね。理想的には赤色になって欲しいけど、実際に取れる信号は緑色のようにブロードになってしまう。
高域強調フィルタをつかえばいいんだけど
計測の度にこのブロード具合が変わったりすると、調整が面倒くさいよね。この信号を、音声さん見ると。「声帯」と「声道」の関係やん。見えるよねっという話。赤色の信号源に声道形状から決まる周波数フィルタをかけたものが緑色なんやろ? それならそのフィルタさえ求まれば、色々手が打てるよね。
スペクトル包洛
上の緑の信号のパワースペクトルを取ると以下の水色のグラフになります。なんかギザギザしてるのが源信号で、フィルタ特性はスペクトルの大まかな形(スペクトル包洛)に出てきます。詳しい事はこの辺のサイトに載っています。
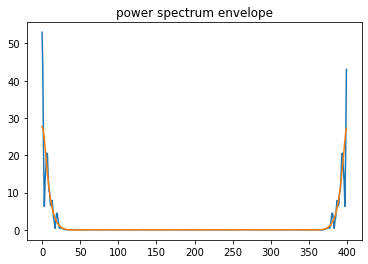
このパワースペクトルの包洛を求めるには、パワースペクトルをフーリエ変換して、高域を切って上げれば良さそうですね。パワースペクトルのフーリエ変換をケプストラムと呼びます。
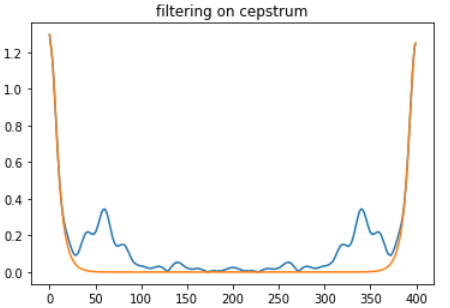
音声処理ではこのケプストラムのうち、グラフの端っこのみを残して、中央を削り取るのですが、一旦こここで我に返ってみましょう。音声じゃありません。これは単に位相情報を消した、実空間での信号でしかないです。欲しいのはピーク形状なので単峰です。なので時間がらループしてるので解りにくいですが、一番デカいピークを切りだせばOKですね!
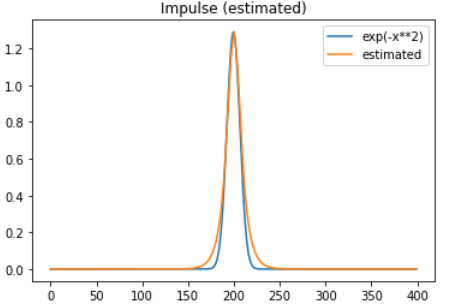
ということで良い感じに単一ピークを切りだして、コレをインパルス応答やと思えばOKでしょう。見易くするために、ピーク位置をグラフの真ん中にもってきて、実際に本当のインパルス応答と比較してみましょう。裾がちょっと拡がっているけれども、概ね太さは一致してます。
あとは逆フィルタかけるだけ
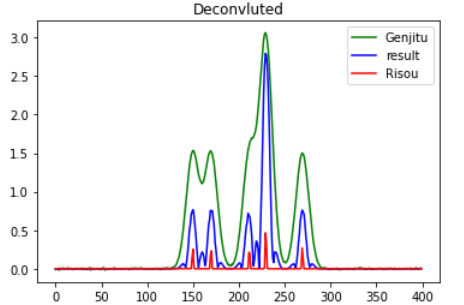
オレンジ色の線として、フィルタが求まったので、あとは逆フィルタをかけるだけですね。といっても時間遅れがないフィルタなのでやることは単純です。フィルタのせいでスペクトル包洛にあるようにパワースペクトルが減ってるので、割り算して戻してやればよいです。ただしスペクトル包洛の中央部分はゼロなので適当に手加減して上げる必要があります。
パワースペクトル包洛をcfだとして観測信号をsimだとします。fft(sim)/cfというふうに1/cf倍しますが、ゼロの部分で無限倍になって都合がわるいです。以下のように20倍程度にリミットをかけて増幅してみました。

緑よりも、青の方が、ピークの位置がわかりやすくなったんじゃないでしょうか?アーティファクトなピークを無視するのに心眼は必要ですが。
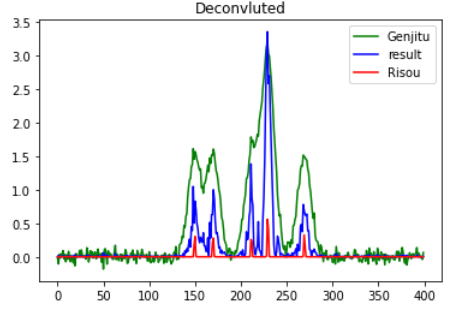
ちなみに、ノイズを10倍にしてもこんな感じ意外と行けます。
おわりに
作図に使ったソースコードははここです。グラフ表示以外のコード部分抜き出すとこれだけの処理です。